Kennismanagement binnen lokale erfgoedorganisaties

Op dinsdag 7 december 2010 was ik uitgenodigd bij FARO, het Vlaamse steunpunt voor cultureel erfgoed voor een presentatie over kennismanagement. Men is er immers van overtuigd dat ook in kleine erfgoedverenigingen een nood is aan kennismanagement. Vaak bulken deze verenigingen van relevante kennis op hun domein, maar komt die kennis niet voldoende aan de oppervlakte.

Vanuit de 3 E's van performantiemanagement probeer ik deze kleine vrijwilligersorganisaties te overtuigen dat ook zij baat hebben bij een professioneler beheer en verspreiding van hun kennis.

• Efficiëntie: zoals beter en sneller (samen)werken, kennis bewaren die dreigt verloren te gaan wanneer medewerkers de organisatie verlaten ;

• Effectiviteit, in functie van het doel van de vereniging en het verbeteren van de resultaten van de vereniging

• Spaarzaamheid (Economy) : verspilling van middelen voorkomen.

Daarvoor suggereer ik het gebruik van enkele web 2.0-toepassingen, zoals (micro-)blogs, wiki's en RSS.

Kennismanagement binnen lokale erfgoedorganisaites

View more documents from Jan Van Hee.

De redenen voor strategische informatiemanagement (2) : innovatie

Informatie is onlosmakelijk verbonden met de levensnoodzakelijke innovatie van elke organisatie, het invoeren van nieuwe ideeën, goederen, diensten en processen.

Stephen P. Robbins en Mary Coulter [Management / Robbins, Stephen P. en Coulter, Mary. – Pearson Education Benelux, 2003. ] beschreven vier clusters van variabelen die de invloed op de innovatie van een organisatie beïnvloeden. Innovatie kunnen we beschrijven als het vermogen om producten, processen of structuren te ontwikkelen of te vernieuwen. Innovatie is een vereiste tot het voortbestaan en groei van elke organisatie. Typisch is dat de informatiehuishouding zich situeert op de vier variabelen. Dit tonen we aan op onderstaand schema :

Te vaak wordt informatie enkel belicht vanuit de systeemvariabele (technologie), terwijl andere variabelen minstens even belangrijk zijn : zo is de structuur belangrijk voor de informatiedoorstroom en zal de cultuur ingaan op het aspect van het kennisdelen. Op vlak van competenties zijn het natuurlijk de kennis en de vaardigheden om met informatie om te gaan die in het oog springen.

De redenen voor strategische informatiemanagement (1) : onzekerheidsreductie

Informatie zorgt er voor dat personen en organisaties gefundeerde beslissingen kunnen nemen. Voor elke strategische of operationele beslissing of voor het sturen van elk proces heeft men informatie nodig. Dit kan gebeuren op strategisch niveau, maar is evengoed noodzakelijk op het niveau van de werkprocessen. Zo zal een manager bij voorkeur de situatie analyseren in plaats van een blinde gok te wagen bij een investering of zal een werknemer niet goed kunnen functioneren wanneer die steeds nieuwe richtlijnen moet vragen bij zijn dagdagelijkse werkzaamheden.

Maar soms kan dit ook zorgen voor een een dilemma : wanneer beschikt een manager over voldoende informatie om een beslissing te nemen ? Bijvoorbeeld : moet een strategische beslissing uitgesteld worden omdat de informatie onvolledig is, maar dan wel met het risico dat een concurrentievoordeel wordt kwijtgespeeld?

De onzekerheidsreductie wordt vooral geconcretiseerd in de context van beslissingssituaties, waarbij informatie het nemen van een besluit moet vergemakkelijken.
Toch zien we in het bedrijfsleven en bij de overheid dat algemeen ondersteunende informatiediensten worden ingekrompen of beëindigd omdat men erop vertrouwt dat iedereen alles nu zelf kan vinden met de huidige informatiesystemen. Dit noemen we "disintermediation" : de verantwoordelijkheid voor het verzamelen van informatie wordt verlegd naar de medewerkers zelf. Er wordt massaal geïnvesteerd in “datawarehousing”, maar de klassieke diensten verdwijnen. Zeldzaam worden de organisaties die nog een bibliotheek, documentatiedienst of archief hebben. Managers kennen de bronnen van hun informatie niet en hebben er vaak ook geen interesse voor voor.

Een grondige aanpak van de informatiehuishouding is echter een voorwaarde tot behoorlijk bestuur. Dit wordt ondermeer aangehaald in de basisprincipes van het “Beter Bestuurlijk Beleid” van de Vlaamse overheid. Als we de principes van “good governance” of deugdelijk bestuur uitwerken, merken we dat o.a. accountabilitiy en het zorgvuldigheidsbeginsel niet zonder een gedegen informatiehuishouding kunnen.

anders presenteren met Prezi

In de voorbereiding van een workshop of presentatie kruipt heel wat tijd, niet in het minst met het vormgeven en organiseren van je slides. Het nadeel van Powerpoint is dat het een volgorde van presenteren vastlegt. En in een dynamische workshop wil je nu net het publiek aan het woord laten en makkelijk naar het onderwerp springen waarover gediscussieerd wordt.

Met Prezi wordt dit een stuk makkelijker. Je bouwt de presentatie op als een mindmap. Dit gaat alvast een stuk sneller dan bij het werken met powerpoint en aanverwanten. Tijdens het presenteren volg je een pad, maar zoom je net zo makkelijk in en uit naar een ander onderwerp waar je op dat moment dieper wil op ingaan.

Her en der noemen ze Prezi al een 'powerpoint-killer'. Ik geloof er wel in. Maar Prezi heeft wel nog een aantal beperkingen zoals het ontbreken van de mogelijkheid om URL's aan een afbeelding te koppelen. Je moet altijd de volledige - soms onleesbaar lange - URL opnemen in je presentatie. En je kan geen 'slides' afdrukken... Maar dat vind ik persoonlijk vooral een voordeel.

Bibliotheek 2.0 : interactieve webdiensten in een bibliotheekcontext on Prezi

De kleren van de Bib

Op vrijdag 1 oktober 2010 hield het Antwerps Bibliotheekcentrum Vrieselhof een gesmaakte studiedag over informatiebemiddeling in openbare bibliotheken. Maarifa mocht ondermeer het toekomstbeeld van die informatiebemiddeling schetsen. Hieronder vindt u de slidecast van deze presentatie.

Bibliotheekcollecties evalueren met de z-score

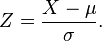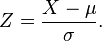
Twee jaar geleden publiceerde ik een artikel over kwantitatieve evaluatietechnieken voor bibliotheekcollecties : "collecties evalueren". Daarin beschreef ik zeer kort de verschillende methodieken en kan men (nog steeds) een Doe-het-zelf-formulier downloaden.

De laatste tijd voel ik steeds meer voor één van de aangekaarte methodieken : de Z-score. Deze methodiek werd niet speciaal ontworpen voor bibliotheekcollecties, maar is een vrij courante statistische methode om verschillende populaties met elkaar te vergelijken. In ons geval worden deze populaties collectieonderdelen.

Iedereen in de bibliotheekwereld is (zou) vertrouwd (moeten zijn) met de klassieke basistechnieken als bezitscoëfficiënt, leenfrequentie en gebruikscoëfficiënt (turnover rate). Deze technieken zijn misschien goed voor basale benchmarktoepassingen en normeringen, maar zijn zeer beperkt in hun toepassing binnen de bibliotheek, omwille van het ontbreken van statistische relevantie. Anders gesteld : wat moeten we met die cijfers ? Wat betekent een turnoverrate van 2,3 voor onze bibliotheek ?

Aan de andere kant van het spectrum hebben we dan de integrale benadering van systemen als het Integraal Collectiebeheer (ICB) (ontwikkeld door Bureau Leemans). Hiermee krijgt men kant-en-klare-collectieadviezen.

Toch kan Z-socere een tussenweg bieden. Het is (uiteraard) veel beperkter dan het ICB-model, maar het biedt in combinatie met goed uitgewerkte collectieprofielen een efficiënt alternatief.
De Z-score is alvast hanteerbaarder dan andere modellen zoals Gütersloh en Doucet-Larbre.

De Z-score is afgeleid van de Use-factor (die dan weer gelijkenissen vertoont met de turn-over-rate). Bij de Use-factor bepaalt men voor elk collectieonderdeel het relatieve aandeel in de gehele uitleen en het relatieve aandeel in de totale collectie. Het eerste getal wordt door het tweede gedeeld.

% uitleningen van een rubriek / % bezit van een rubriek

Indien het bekomen getal groter is dan 1 is het aanbod in die rubriek te klein, indien het kleiner is dan 1 is het aanbod te groot.

Het grote probleem is echter dat de Use-factor (zoals alle berekeningen op basis van percentages en gemiddelden) zeer gevoelig voor uitschieters. Dit kan bijvoorbeeld een schrijver of een onderwerp zijn die een hype veroorzaakt. Bij gemiddelden kunnen die uitschieters geneutraliseerd door gebruik te maken van de standaard-afwijking (zoek maar eens STDEV op bij de Excel-functies).

Dit is ook wat de Z-score gebruikt om een evenwichtig beeld te verkrijgen van de collectie. Deze methodiek gebruikt de Use-factor voor elk collectieonderdeel, maar trekt daar de gemiddelde use-factor van de totale collectie af en deelt dit door de standaardafwijking.

Een evenwichtige collectie ligt dan tussen -1 en 1.

Dries Calleeuw maakte een mooie case over een muziekafdeling en hier vindt u een leeg formulier voor eigen gebruik.

Zoals eerder gesteld moet deze werkwijze gecombineerd worden met duidelijke collectieprofielen en een duidelijke beleidsvisie (zie mijn vorige post).

Een visie op collectiemanagement in openbare bibliotheken

Bibnet en de provincies zetten de laatste jaren sterk in op een professionele omkadering van het collectiemanagement. Initiatieven als Integraal CollectieBeheer (ICB) van Bureau Leemans in de provincies Antwerpen en Oost-Vlaanderen beantwoorden aan deze trend.

Zelf ben ik op dit moment bezig met een opleiding collectieontwikkeling voor de Bibliotheekschool van Gent en een praktische opleiding "collectieplannen" voor de provincie Oost-Vlaanderen.

Opvallend is dat het werken met collectiedoelen en -profielen en marktgegevens minder problemen biedt dan verwacht. In de openbare bibliotheken is efficiëntie geen loze term. Even opvallend is evenwel dat het uitschrijven van een visie op collecties minder evident is.

De visie op collecties en collectiemanagement zou je kunnen omschrijven als de grijze, maar noodzakelijke, zone tussen de missie van de bibliotheek en de collectiedoelen.

Grijs omdat het conceptioneel is en dus wat vaag, het mag ook niet concreet zijn omdat een visie per definitie tijdloos is. De visie moet breed genoeg is om in te spelen alle mogelijke opportuniteiten en evoluties, maar moet wel wortelen in de realiteit van organisatie. (Strategie en organisatie van publieke organisaties /Sebastian Desmidt, Aimé Heene). Dus woorden als "dvd", "i-pod" of "e-book" kunnen dus niet gebruikt worden in een visie omdat ze een beperkte houdbaarheid in zich dragen.

Noodzakelijk omdat dit de link is tussen de mandaten en de missie van een bibliotheek en de concrete collectiedoelen.
Terwijl dat de missie zeer kort zal situeren WAT je gaat doen en WAAROM, gaat de visie in op de HOE-vraag. De visie moet trouwens duidelijk omschreven zijn voor men bijvoorbeeld instapt in samenwerkingsverbanden en collectiemanagementsprojecten.

Maar hoe pak je dit nu praktisch aan ?

Visie kun je associëren met visionair, daarom is het een goed idee om als eerste stap een "toekomstvisie" uit te schrijven : hoe zal je ideale collectie er uit zien binnen pakweg 50 jaar. Hoe zullen die collecties er dan uitzien ?
Beschrijf de elementen die tot succes zullen leiden : waarom zullen bibliotheekcollecties nog belangrijk zijn in de toekomst ?

Beschrijf ook de drijfveren voor het collectiemanagement. Enkele klassieke uitgangspunten hebben we hieronder opgelijst :

• Pluriformiteit
• Actualiteit
• Evenwicht
• Betrouwbaarheid
• Klantgerichtheid
• Verscheidenheid

Wat vaak vergeten wordt is dat de ideale situatie ook begrenzingen kent. Beschrijf daarvoor ook de grenzen en mogelijke uitdagingen aan de collectievorming. Enkele aandachtspunten :

• Juridische grenzen
• Ethische en maatschappelijke grenzen
• Moeilijkheidsgraad
• Taal
• Afstemming andere bibliotheken
• Intrinsieke kwaliteit

Een collectieplan voor openbare bibliotheken in Oost-Vlaanderen

View more presentations from Jan Van Hee.

Als e-mail niet was uitgevonden...

Geen enkele ICT-toepassing heeft onze manier van werken zo beïnvloed als e-mail. Maar e-mail is zo allesoverheersend geworden dat we zelfs een 'e-mailloze dag' nodig hebben om op adem te komen :-)

Als experiment heeft Google de manier van elektronisch communiceren helemaal herdacht. Onder het motto 'wat als e-mail nooit was uitgevonden, hoe zouden we dan nu communiceren?' bedachten ze Google Wave.

Google Wave ademt Web2.0: blog, chat, wiki, realtime informatie, documenten delen ... Geen toevloed van e-mails die de wereld rondgaan, waarop gereplyed wordt, die geforward worden, waarin bijlagen rondgestuurd worden, ... meer. Met Google Wave worden berichten op een centrale server geplaatst en kunnen mensen participeren aan een Wave.

Google Wave heeft in theorie alle ingrediënten om de nieuwe manier van communiceren te worden en van e-mail een relikwie uit de vorige eeuw te maken. Maar of dat in de praktijk zo zal zijn valt nog even af te wachten. Een mens is nu eenmaal een gewoontedier, nietwaar.

En toch. Google Wave is toch wel een intrigerende toepassing. Google Wave is nog steeds in test en kan enkel op uitnodiging (iemand nog eentje nodig? ik heb er nog een paar) uitgetest worden.

Is Google Wave nieuw voor u? Neem dan zeker even de tijd om onderstaande video's te bekijken.





En wat denkt u nu? Zal Google Wave e-mail vervangen?